Maths is providing new ways to make sense of biology

In the early 2000s, a fierce debate was raging among health practitioners about when to start HIV patients on antiretroviral therapy. The standard approach at the time was to delay treatment until the disease had progressed to a critical stage. However, emerging mathematical models challenged that dogma. They showed that the virus could silently ravage the immune system even when the patient didn’t show symptoms. These theoretical studies ultimately led the Centres for Disease Control and Prevention, USA, to change treatment guidelines – asymptomatic patients were also given antiretroviral therapy. This dramatic shift saved at least two million lives in the USA alone.
It was this story that hooked Narendra Dixit, Professor at the Department of Chemical Engineering, on mathematical and computational modelling. To him, it illustrated the power of modelling to illuminate the complexities of biological systems.
At its core, modelling is all about capturing the essential components and interactions of a system – whether it’s a single cell, an organ, or an entire ecosystem – in the language of mathematics. By distilling these intricacies into equations and computer simulations, researchers can unearth hidden patterns, predict the outcomes of different interventions, and guide the design of new experiments. It’s like constructing a virtual lab where you can test out ideas and make predictions about what could happen in the real world.
Modelling is like constructing a virtual lab where you can test out ideas and make predictions about what could happen in the real world
Since 2005, Narendra’s lab has been using mathematical models to study infectious diseases, from investigating how HIV hijacks the immune system to designing better vaccination strategies for COVID-19.
One of their models focused on understanding the puzzling outcomes of hepatitis C treatment with a drug called interferon. Before 2012, hepatitis C was treated using interferon, but it worked in only about 50% of patients. Narendra’s team set out to understand why.
They developed a mathematical model of the complex network of interactions between the hepatitis C virus, the immune system, and the drug. The model revealed that the effectiveness of interferon depended on the delicate balance between the strength of the patient’s own response to interferon and the virus’ ability to suppress it.
“It turns out, if you get into the details, that there was a network of interferon signalling [in liver cells] that displayed multiple steady states, which was at the heart of this outcome of treatments,” Narendra explains.
This phenomenon, known as bistability, means the system can exist in two stable states: one where interferon controls the virus, and another where the virus persists despite interferon.

Using a model of viral kinetics, the researchers made a crucial discovery: there’s a critical threshold in the proportion of liver cells that respond to interferon. When the fraction of cells refractory (resistant) to interferon in a patient exceeds this critical value, treatment fails.
In patients where the proportion of interferon-resistant cells is below the critical threshold, the treatment can effectively control the virus. However, in patients where this proportion exceeds the threshold, even high doses of interferon are ineffective.
The model also suggested a new approach: combining interferon with drugs that directly attack the virus. By reducing the overall viral load, these drugs can lower the number of interferon-resistant cells below the critical threshold, making the treatment effective again. This prediction aligned with the later success of combination therapies using both interferon and direct-acting antivirals.
By translating complex biological processes into mathematical equations, Narendra’s team uncovered hidden patterns that could lead to more effective treatments for diseases like hepatitis C.
Defeating disease with data
A major problem in biology today is making sense of the deluge of data being generated by experiments, realised Nagasuma Chandra, Professor in the Department of Biochemistry, when she began her foray into mathematical biology two decades ago.
“There’s data coming from all levels – molecules, cells, tissues, organisms,” she says. “To synthesise it and find meaning in it, you need mathematical modelling. There’s no other way.”
Nagasuma’s lab specialises in building multi-scale models that can zoom in and out on biological phenomena. They used this approach to untangle one of the most vexing problems in medicine – the rise of antibiotic-resistant bacteria.
‘There’s data coming from all levels – molecules, cells, tissues, organisms. To synthesise it and find meaning in it, you need mathematical modelling’
Nagasuma’s team developed a mathematical model to simulate the evolution of drug resistance in the tuberculosis bacterium. By training their model on data from painstaking experiments that exposed the bacteria to different antibiotics over multiple generations, they were able to pinpoint a previously unknown mechanism of resistance.
“We found that resistance doesn’t arise from a single mutation or a single gene, but from the complex interplay between different biological scales,” she explains. “It emerges from the dynamic feedback between the metabolic state of the bacterial cell, its stress response pathways, and the external environment.”
This type of holistic understanding is something that traditional, reductionist approaches to biology often miss – they typically focus on individual parts or processes. Mathematical models, on the other hand, excel at capturing emergent properties that materialise when all these parts come together. Learnings from these models can be taken back to the lab to test out new hypotheses, Nagasuma suggests.
Unravelling complexities of cancer
Complex interplays between different cell types, molecular pathways, and environmental factors also underpin the development of diseases like cancer. Mohit Kumar Jolly, Associate Professor at the Department of Bioengineering, has been using mathematical oncology to dissect these dynamics.
A focus of his work is the epithelial-to-mesenchymal transition (EMT), a process by which cancer cells can detach from their neighbours, migrate to other parts of the body, and establish new tumours. Epithelial cells line the surfaces of our organs and body cavities, forming a protective barrier and maintaining the structure of tissues. They are typically tightly packed together and anchored by strong adhesive molecules. Mesenchymal cells, on the other hand, are more loosely organised and migrate freely, which is important for processes like wound healing and embryonic development. EMT was long thought to be an all-or-nothing switch – either cells were epithelial or they were mesenchymal.
“But we found [using models] that cells can actually exist in a continuum of states between epithelial and mesenchymal,” Mohit explains. “And it’s these hybrid states that are the most dangerous in terms of driving metastasis (the process of cancer cells migrating and invading other organs).” This is because hybrid cells inherit the worst of both cell types – they can adapt and travel more easily to other body parts.
This insight has profound implications for cancer treatment. Rather than trying to block EMT entirely, therapies may be better off targeting the most metastatic cells while allowing other cells to remain epithelial. Mohit’s lab is now using mathematical models to predict how different drugs might affect this delicate balance and to identify new therapeutic strategies.
Models are also helping researchers like Soundharya Ramu, a second-year PhD student at the IISc Mathematics Initiative (IMI), link our understanding of disease to clinical outcomes for patients. Working with Mohit and Annapoorni Rangarajan, Professor at the and Genetics (DBG), she is using multi-scale modelling to explore how hypoxia (a low oxygen environment) influences cancer cell activity and its spread.
Her models incorporate data from experiments that profile the molecular landscape of cancer cells and figure out how they change over different tumour regions. By simulating how these molecular changes play out over the space occupied by the tumour, she is attempting to predict how tumours will evolve and identify the most promising treatment strategies.
“What I find most exciting about this work is the ability to integrate data from so many different levels and build a coherent picture of the system as a whole,” Soundharya says. “It’s like putting together a jigsaw puzzle where you have to figure out how all the pieces fit together to create the final image.
Mimicking nuances of neurons
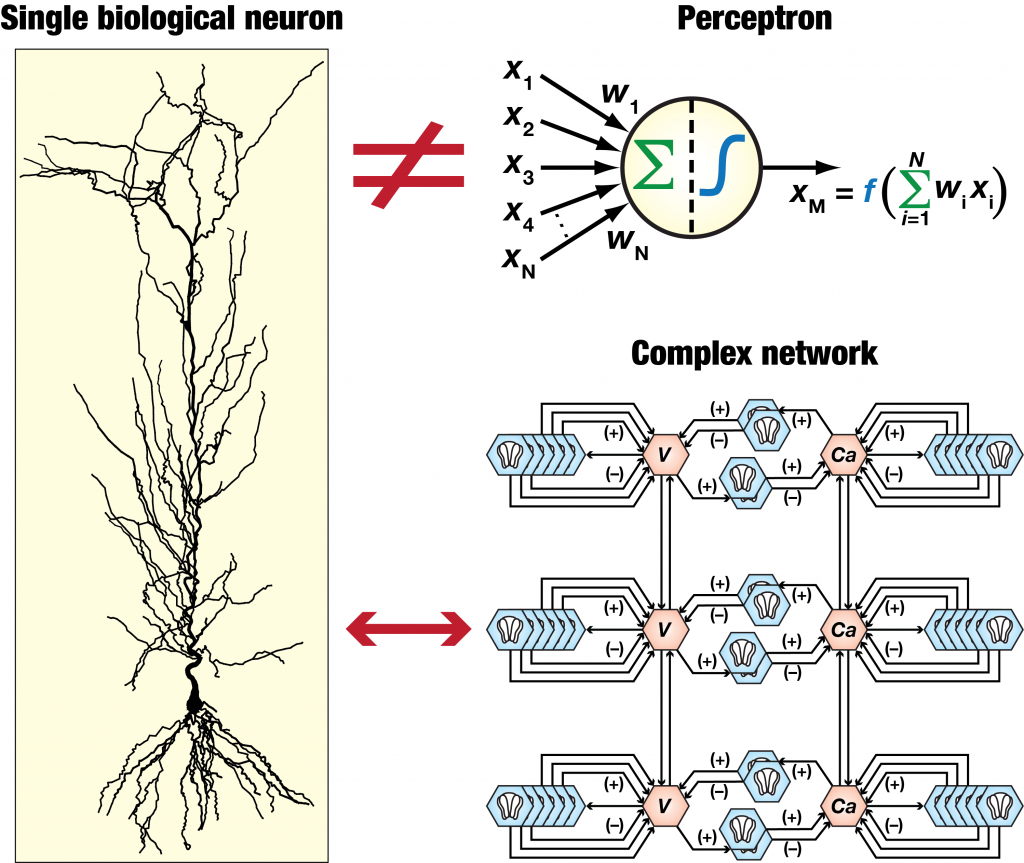
As an electrical engineering student, Rishikesh Narayanan, Professor at the Molecular Biophysics Unit (MBU), was drawn to neuroscience by the prospect of studying the brain as the ultimate computing device. When he delved deeper into the biology of neurons, a major type of cell in the brain, he was struck by their immense diversity. “Two neurons in the same brain region that have the exact same kind of activity can achieve it through completely different mechanisms,” Rishi says. Neurons are also noisy – they generate a lot of signals at random.
This is why when Rishi’s lab builds computer models of individual neurons as well as networks, they ensure that they account for both diversity and randomness. By comparing the behaviour of models with slightly different properties of neurons, they’ve been able to pinpoint key ion channels and signalling pathways that shape the activity of different cell types. “There was one particular potassium current that nobody would have thought was important based on the biology alone,” he recalls. “But our model predicted that it would have a huge effect on multiple features of the neuron’s activity, and subsequent experiments bore that out.”
A key challenge in building such models, he points out, is to figure out which parameters matter for a given phenomenon, and which ones are just noise. “You can’t just build a single canonical model of a neuron and expect it to capture all the important features,” he says.
Blurring boundaries
Today, more and more researchers are embracing the use of mathematical models to guide every stage of the scientific process, from hypothesis generation to data analysis. These models can not only help solve specific problems but also have the capacity to change the way we think about life itself. The convergence of maths and biology is opening up new frontiers in fields like personalised medicine, synthetic biology, and regenerative medicine.
But there’s a hitch: In India, maths and biology have long been cordoned off from each other. As high school students, how many of us have been asked: Do you want to become an engineer or a doctor? Do you want to study mathematics or biology?
“There is a dichotomy in our educational system – in 11th and 12th grade you are supposed to choose between maths and biology streams,” explains Rishi. As a result, students somehow think that if they take biology, they are incapable of doing maths, or vice versa, he says. “We need to create a scientific ecosystem where students feel empowered to follow their curiosity across disciplinary boundaries,” says Narendra. “The most exciting discoveries happen when people from different backgrounds come together and share their unique perspectives.”
‘We need to create a scientific ecosystem where students feel empowered to follow their curiosity across disciplinary boundaries’
Rishi echoes this as well; he suggests that the change has to happen at the school or early university level. “I make it a point to try and give a talk in small colleges wherever I visit … just because you have chosen biology or mathematics does not imply you cannot learn the other. Go where the question takes you.”
“We need to systematically train students to be bilingual in maths and biology from an early stage,” adds Mohit. “The major challenge right now is developing a critical mass of people who can speak both languages fluently.”
As the boundaries between disciplines continue to blur, it is increasingly clear that mathematics is not just a tool for physicists and engineers, but an essential language for deciphering the complexities of life itself.
Amruth Deepak Bhat is an MTech student in the Department of Bioengineering, IISc and a science writing intern at the Office of Communications