Why some enjoy the subject for what it is

Let us begin with an unusual counting puzzle. Imagine two blocks labelled 1 and 2, next to each other on the ground beside a wall. Assume that the ground is frictionless, and that the blocks will not lose energy when they hit each other or the wall. B1 is closer to the wall, and both blocks weigh 1 kg. This is the scenario that YouTuber Grant Sanderson, who runs the popular 3Blue1Brown maths channel, sets up in one of his videos.
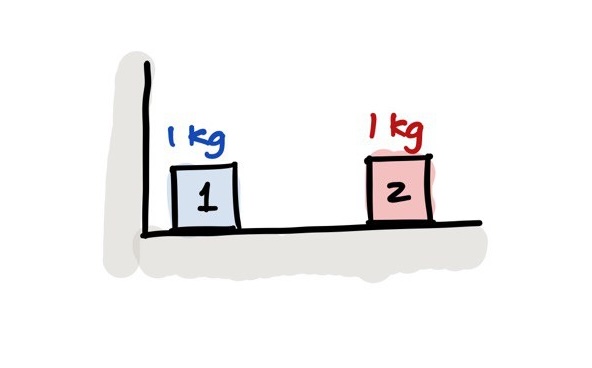
Now, imagine pushing B2 towards B1 and hearing a clack as they hit each other. B2 pushes B1 to hit the wall, resulting in another clack, and B1 rebounds from the wall to hit B2 again, pushing it away. This will result in three total clacks.
What happens if the weights change? Say block 2 weighs 100 kg while block 1 remains 1 kg. Now, B2 hits B1, B1 smacks against the wall and returns to hit B2 again; but since B2 is heavier, it will not move away so easily. B1 will end up bouncing between B2 and the wall again and again, ratcheting up the clack count to 31.
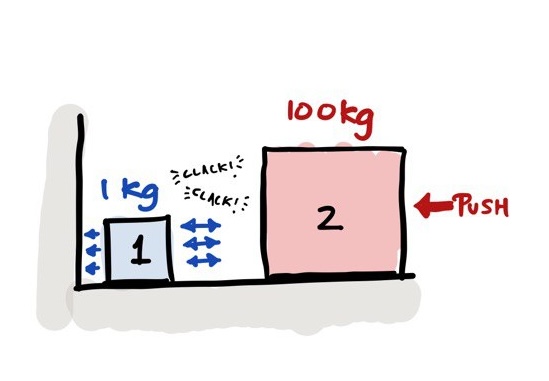
If you keep increasing block 2’s weight, to 10,000 kg or 106 kg, the number of clacks will keep increasing, to 314 or 3,141, respectively. If block 2 weighs 108 kg, the clack count is 31,415.
Do you see a pattern yet?
Somehow, as one block gets heavier by a factor of 100, the ensuing number of clacks matches the digits of, you guessed it – pi. But we only know of pi being related to a circle. Why should these clacks – from two blocks hitting each other on a flat, frictionless one-dimensional surface – compute pi?
“What follows is a detective story of tracking down the circle … but not because it is useful,” says Grant later in a TEDx talk. “ [It’s] because the story has drawn you in.”
Unsolved mysteries like these are what draw mathematicians to their muse, even if they don’t seem to have any direct relevance in our daily lives. They can be about finding intriguing patterns in numbers, studying symmetrical shapes in the world around us, or just finding mind-boggling connections across different areas of maths.
That’s not to say that people don’t work on “practical” maths, like the equations and processes underlying stock prediction models, neural networks, or weather forecasts. As Grant mentions in his talk, even the study of prime numbers, as “pure and platonic as it may seem”, has applications in modern cryptography. But this is not necessarily why some mathematicians study maths.
Harish-Chandra, an influential mathematician from India who worked at the Institute of Advanced Studies, Princeton, USA, succinctly summed up his thoughts on why studying maths is worthwhile. He writes: “Music is not useful in any way except that it makes us feel good. Similarly, the main attraction of mathematics lies in the fact that it is beautiful.” He apparently scribbled this on the back of one of his papers, according to CS Aravinda, Professor at the Tata Institute of Fundamental Research (TIFR).
‘If you look at the language [of maths] itself … it responds to something fairly deep and fundamentally aesthetic in us’
Mahan Mj, Professor of Mathematics at the Tata Institute of Fundamental Research (TIFR), Mumbai, relates to this aesthetic appeal. He explains how doing pure mathematics can, in part, be compared to enjoying Shakespeare. “Mathematics has a dual life. It is the language of science; one needs mathematics to lend precision to science,” says Mahan. “But if you look at the language itself… it responds to something fairly deep and fundamentally aesthetic in us as well.”
In Grant’s talk, I can almost feel his excitement as he describes how some maths problems have all the components of a story. He likens the colliding blocks example to a good mystery novel. The clacks somehow adding up to pi is tantalising evidence that something deeper is at play, but finding and proving the connection needs some deduction. “It appeals to emotion, has comedy and some notion of characters, a mystery you need to see resolved,” he says. “[It can] really pull you in for the math that it is now, not what it promises to give you later.”
What is so mysteriously beautiful about maths? To find out, first, we will need to journey into the world of one of its key ingredients – numbers.
Pretty Patterns
Apoorva Khare, Associate Professor at the Department of Mathematics in IISc, is always on the lookout for intriguing patterns in maths. When I met him, he was practically bouncing on the balls of his feet as he explained one simple example on a blackboard.
“Suppose I tell you to multiply any two consecutive odd numbers, and then add one, you will always get a perfect square,” he says.
Try this:
(1 x 3) + 1 = 4 = 22
(3 x 5) + 1 = 16 = 42
(5 x 7) + 1 = 36 = 62
(7 x 9) + 1 = 64 = 82
Not only do we get a perfect square each time, but the result is also the square of the even number in between the two odd numbers (2 between 1 and 3, 4 between 3 and 5, and so on). There, the pattern emerges.
But finding the pattern is just the first step. One must then prove that the pattern exists for all possible numbers. “Of course, I’m not going to verify every pair of odd numbers; that will take forever. So, instead, can I find a general formula that holds for all these things?” explains Apoorva. “You can verify all of them simultaneously using one calculation in mathematics.”
For this, he explains, we can exploit the power of variables – symbols that represent some changing or varying quantity. Instead of juggling an infinite list of numbers, let’s just take a number which we can call x, our variable. Now we just need to remember some maths we learned in school, and prove that multiplying x-1 with x+1 (the consecutive odd numbers) and adding 1, will always give the square of x (the central number).
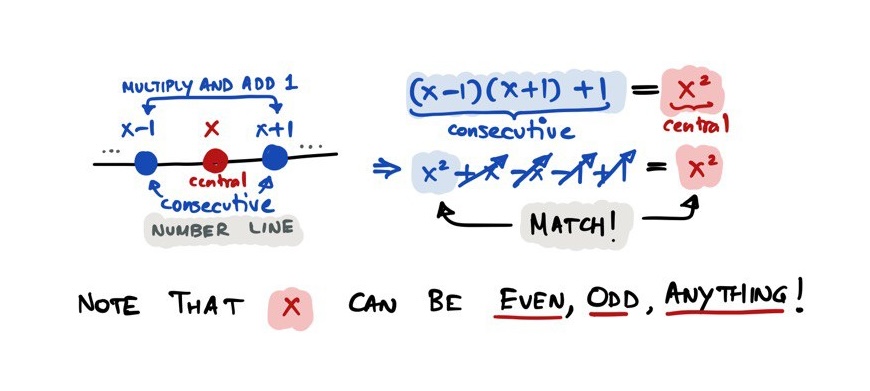
You will also realise that this pattern holds for all numbers; as x can be any number you like, the proof always holds. Even if you multiply two consecutive even numbers and add 1, you’ll get the square of the odd number in the middle.
“My love for mathematics started with this [finding patterns]. When I was in school, I would do these kinds of things – try to put variables and symbols in and then just [prove] the general [case],” says Apoorva. “Suddenly, you see the truth underlying infinitely many facts. Finding the underlying truth of these things, or why something is true, has always appealed to me.”

The above example is a simple pattern with a straightforward proof. But there are many open maths problems that mathematicians have been trying to solve for centuries, with little success. Some of these problems are related to prime numbers.
Mathematicians have eternally been perplexed by primes – numbers that can only be divided into whole parts by 1 and the number itself. “Primes are like the elements [in chemistry]; everything else is built out of them,” says Jordan Ellenberg, Professor of mathematics at the University of Wisconsin-Madison, USA. “Every number is made up of primes … so if you understand them, then you understand a lot of other stuff too.”
In 1742, German mathematician Christian Goldbach wrote a series of letters to another mathematical great, Leonard Euler. In those letters, he outlined the famous Goldbach’s Conjecture, which states that every even number greater than 2 is a sum of two prime numbers. We can test this in our heads for smaller numbers, like 8 being a sum of 3 and 5, 12 being a sum of 5 and 7, 18 being a sum of 11 and 7 and so on, but mathematicians haven’t yet proved that it is true for every even number that exists.
Another famous unproven statement from around 1849 is the Twin Prime conjecture, which states that there are infinitely many prime numbers that are separated by two, like 5 and 7, 11 and 13, or 599 and 601 – again, we don’t know if this holds true for all numbers. Many mathematicians are determined to prove such centuries-old conjectures.
“Sometimes, [if] I find the question interesting, just for the sake of it, I’ll stop everything else and work on that for a few days,” says Apoorva. “I always try to do the maths that appeals to me. Maybe that’s what inherently is called beauty here – [it’s in] the eye of the beholder.”
The dangerously alluring Collatz Conjecture
The Collatz Conjecture, also called the 3n+1 problem or the hailstone problem, looks so simple that even school kids can play around with it. But for mathematicians, it is a quagmire – many have gotten stuck for years trying to prove it; some advisors even warn their students to stay away from it. The conjecture became so notorious that in the 1960s, people even joked that it may be a conspiracy to slow down American research.
Here’s the problem. Take any number n, and if it is even, cut it in half (n/2). If it is odd, triple it and add it to 1 (3n +1). Keep doing this, again and again, with every number you get, and you will eventually end up in a never-ending loop around 1. The idea is to prove that all numbers end up at 1.
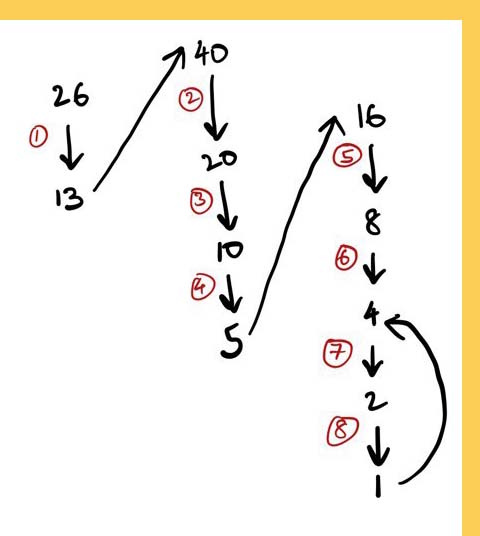
Take 26.
So, 26 goes down to 1 in about eight steps, reaching a maximum of 40 along the way. Intriguingly, just the next number 27 takes a whopping 110 steps to ultimately make its way down to 1, even reaching a massive 9,232 in its journey.
Just like hailstones keep bouncing about collecting more water in the clouds but eventually crash down to the ground, Collatz conjectured that no matter which natural number you start with, you will always land at 1 – only the number of steps varies. Computers have tested this for numbers having up to 18 zeroes, and found that it ends up at 1, but a full proof – which can tie in all the infinite numbers into one neat explanation – has eluded mathematicians for decades. Even Terence Tao, professor of mathematics at University of California, Los Angeles and widely regarded as one of the best mathematicians of our time, hasn’t been able to prove it completely, yet, although, he did edge close to cracking it in 2019.
Surprising shapes
Sarah Hart, Professor Emerita of Mathematics at Birkbeck, University of London, loves maths because she believes it can help us understand things around us. “[It] can explain how and why it is that the natural world coalesces on really beautiful, symmetrical, mathematical-looking structures,” she tells me.
‘[Maths] can explain how and why it is that the natural world coalesces on really beautiful, symmetrical, mathematical-looking structures’
Just like numbers, the world around us is a treasure trove of beautiful patterns – in structure and symmetry – all of which offer many problems for mathematicians to sink their teeth into. To understand this better, we need to swing towards geometry, or the study of shapes.
Rukmini Dey, Associate Professor of mathematical physics at the International Centre for Theoretical Studies (ICTS), Bangalore, studies the geometry of surfaces found naturally around us. She finds herself impossibly intrigued by how such surfaces are always optimised.
One such example is a minimal surface. You might have heard about how the shortest path between two points is a line. Similarly, a minimal surface is a surface that covers the least area within some closed curve in space.
Take blowing bubbles and soap films. When you dip a wire loop into a soap solution and lift it out, you will see a thin soap film clinging delicately between the edges of the loop. The loop here is the closed curve, which acts as a boundary – the soap molecules will always try to stay within this boundary and minimise the area that they occupy. The best shape for that is a thin film.
“Of all surfaces which are spanning that curve, the minimum surface is the one which has minimum area,” explains Rukmini. Just like soap films, soap bubbles also try to optimise the surface area under some constraint. But they try to minimise the area around a fixed volume (three-dimensional) and end up always forming a sphere.
Fascinating Fractals
Fractals are infinitely complex structures, and many have this unique property of “self-similarity” or zoom symmetry. The further you zoom into these structures, you’ll see that they never seem to get simpler – they are made up of smaller and smaller structures that look exactly the same as the original one you started zooming into. The alveoli (air sacs) in our lungs, ferns, trees, rivers, and even lightning strikes, are all fractal in shape.
But self-similar fractals are the ideal case. Any curves or surfaces that are rough or jagged are fractals – shapes that are neither two nor three dimensional, but hover somewhere in between.
Think about a crumpled-up ball of paper. A sheet of paper is roughly two-dimensional, and a perfect paper sphere would have three dimensions. But a scrunched up ball of paper is a roughly 2.5 dimensional fractal – it holds more space than a sheet of paper, but less than a perfect sphere.
Now zoom out further, and imagine the coastline of any country. India’s jagged coastline is a fractal with a dimension of about 1.13 and Britain’s, which is “rougher” than ours, is a fractal of 1.21 dimensions.
As Benoît Mandelbrot writes in his 1982 book The Fractal Geometry of Nature, “Fractal geometry is not just a chapter of mathematics, but one that helps every man [person] to see the same world differently.”
Soap films and bubbles are shapes that we can clearly see around us, but what about some shapes that are a little more abstract?
Imagine a point on the circumference of a wheel. As the wheel rolls along on a flat ground, this point will carve out a shape in space. That shape is called a cycloid.
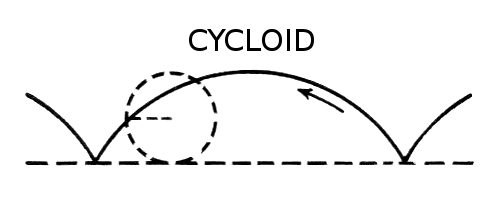
The properties of this curve are so beautiful, writes Sarah in a New York Times opinion piece, that it was even nicknamed the “Helen of geometry.” The moniker was inspired by the Greek mythological character Helen of Troy, who was said to have “a face that could launch a thousand ships” and whom the legendary Trojan War was fought over.
For Sarah, however, the cycloid’s beauty arises from how it manages to slide into different, unexpected scenarios.
“One of the things that we all love in mathematics,” she explains in a podcast called My Favourite Theorem, “is when something you’ve studied over here reappears in a completely different context.”

Spirals in nature
Another shape famously associated with nature is the Fibonacci spiral. To understand what that is, let’s delve a bit deeper into the famous Fibonacci sequence – 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, and so on. Each number in this sequence is the sum of the previous two numbers.
For numbers higher than 5, if you take a number in the sequence and divide it by the previous number, you will get a ratio equal to about 1.6. As the numbers get higher, this ratio becomes closer to 1.618, called the Golden Ratio. Remember this ratio.
Now, make a series of squares, where the length of each square is a Fibonacci number. Then, run an arc through the squares. The resulting spiral is the Fibonacci spiral, or the Golden Spiral. Each time this spiral makes a 90 degree turn, it widens ever so slightly. It turns out that it widens by roughly a factor of 1.618, the Golden Ratio. A chameleon’s tail, seeds in a sunflower, galaxies, nautilus shells – all look somewhat like this spiral.
But not all spirals in nature are Fibonacci spirals. “The reason you get spirals [in a nautilus shell] is because of the way that the shell grows – it starts off tiny, and then as it grows, it creates new material while also rotating,” Sarah explains. “Only some shells actually have that exact [Golden Ratio] growth rate.”
It turns out that if you model this kind of growth and rotation mathematically, you get what is called a logarithmic spiral. This need not always expand by a factor of exactly 1.618, and hence some objects – like galaxies and most nautilus shells – need not always follow the exact Golden Ratio.
Connecting the dots
One major aspect of maths that makes it beautiful, according to Harish-Chandra, is “depth”. He writes, in his notes, that maths leads to an “establishment of an intimate connection between two facts where none seemed at all likely.”
We see this in Dutch mathematician Christiaan Huygen’s story. Sometime in the 1600s, Christiaan wanted to make a more accurate clock than what was around at the time. He came up with the pendulum clock, in which, after making a small approximation, one can assume that it takes the same time for the pendulum to swing back and forth, no matter what height you release it from. But the small approximation niggled at him. Is there any curve that genuinely has this property, he wondered, that no matter where one releases a particle on this curve, it slides down to the bottom taking the same time, every time?
He eventually figured it out. The solution to this tautochrone problem (which means “same time” in Greek), actually turned out to be a cycloid.
“We have an arch; you’ve got to turn the arch upside down. And wherever you release a particle from the top of the [upside-down] cycloid, it will reach the bottom in exactly the same time,” explains Sarah in My Favourite Theorem. “[It’s] what the pendulum almost does … but doesn’t quite [fully] do.”
A few years later, mathematician Johann Bernoulli publicly posed a related problem, called the brachistochrone problem. Imagine two points A and B, with B somewhat diagonally below A, and you roll down from A to B. What kind of curve should connect A and B such that you reach B in the shortest time?
At first glance, a line pops into mind. But note here that it’s not asking for the shortest distance, but the least time. Sliding down a line might help you accelerate downwards, but if the line curves a bit at the start, you might get a bit of a head start and reach down even faster.
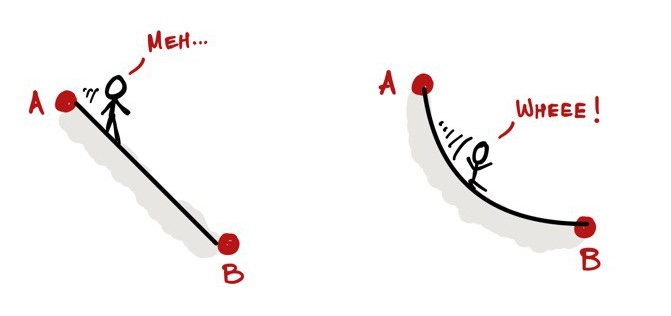
Lots of famous mathematicians submitted their answers to this problem, but one anonymous entry seemed to have the most elegant and beautiful solution. It was, as you may have guessed it, a cycloid. And the anonymous person turned out to be Isaac Newton.
“You’ve got this amazing curve [the cycloid], which is a natural idea. And then it suddenly also can solve these totally different questions about particles rolling down in the quickest time or taking the same time,” says Sarah in My Favourite Theorem. “That is why I love the cycloid so much.”
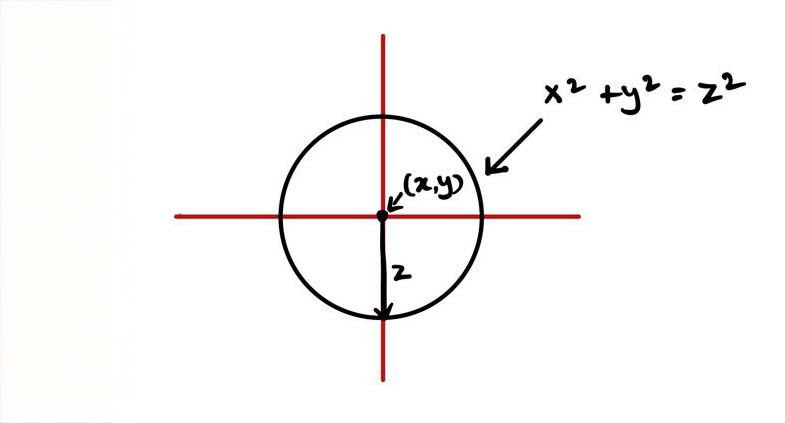
Even the circle can be thought of in different scenarios, wherever there is some notion of distance, according to Jordan. “What I like about a circle is that it has such a nice algebraic description – it’s the set of points at a fixed distance from a given point,” he explains. The equation of a circle is x2 + y2 = z2, where x and y tell us where the circle’s centre is and z is its radius.
“You could talk about it even in a context like genetic distance. If I want to look at the list of my relatives who share at least 1/8th of their genetic material with me, that’s a circle, right?” he adds.
He is also amused by how the constants of a circle, like pi, come up in unexpected places. “They are like mathematical celebrities,” he says, with a laugh. “… coming up again and again in different contexts.”
Rounding off
Circling back to Grant’s blocks in the beginning, if we were to now tease out a connection between the blocks hitting each other and counting pi, how would we go about it?
For that, we will need to invoke a bit of high school physics.
Kinetic energy: ½ mass (m) X velocity (v) squared = ½ mv2 Law of conservation of energy: Total energy of the two blocks always stays constant.
In the simplest case of both blocks having the same mass m, let’s say their velocities are v1 and v2 respectively. Then, no matter how many times they collide, their combined energies will be constant. Let’s now find the link.
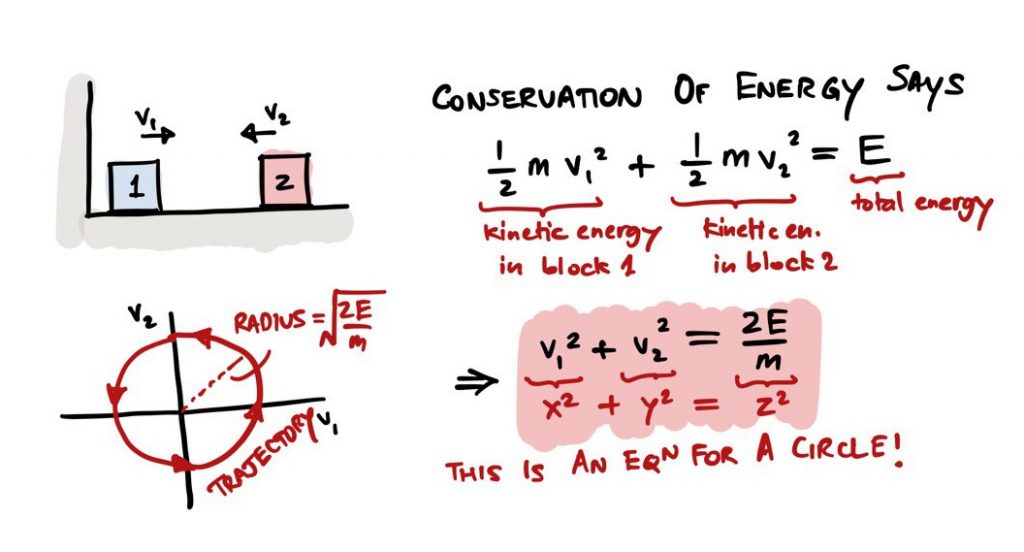
And that is how colliding blocks connect to a circle, mathematically. If you look closely, you’ll realise that we took a pattern – one that naturally emerged from moving blocks – and brought it into the context of geometry and shapes.
It takes more maths to go from the circle to pi, but even without that, just by finding the circle, we have solved a part of this little detective story. The beauty of maths, independent of its potential uses, is precisely in this process – of discovering hidden patterns and uncovering unexpected connections.
“People perhaps misunderstand mathematics as just doing really difficult calculations, but for me it’s all about symmetry and pattern and structure,” says Sarah. “All humans have a natural affinity for them, so I think we are all mathematical thinkers.”
Mathematics in music
Mathematical patterns are also found in music. As French mathematician Gottfried Leibniz once said, “Music is the pleasure the human mind experiences from counting, without being aware that it is counting.” When we enjoy the feeling of a rhythm or are drawn to patterns in melodies, we are actually counting, almost subconsciously. “We enjoy a melody which has parts that repeat – we’ll sing something and then we sing it again,” explains Sarah. Even when it comes to harmonies, there is a mathematical explanation as to why some notes sound good together, according to Sarah. For example, two notes exactly an octave apart sound very harmonious together, and that is mostly because going up an octave is exactly doubling the frequency of the note. A lot of melodious music intervals – the pitch difference between two notes – are based on simple fractions. “Mathematics is a language that is really perfectly suited to describing patterns, that is why it’s good at describing beautiful things,” Sarah says.
(Edited by Ranjini Raghunath)




